My research interests are in low-dimensional topology and
representation theory. In particular, I am interested in
topological quantum field theories (TQFTs) and higher structures related to
link homology theories, and the exploration of their deep
connections to (higher) representation theory and
mathematical physics. I also enjoy applying topological and
combinatorial tools to solve problems in representation
theory.
30) A note on general linear link homology

This expository note outlines why it is sometimes useful to consider the
bigraded type A link homology theories as associated with the Lie algebras gl(N) instead of sl(N).
Contributed to the proceedings of the conference Knots, Quivers and Beyond' (Feb 18th to 21st, 2025).
29) Perverse schobers of Coxeter type A

We define the concept of an An-schober as a categorification of
classification data for perverse sheaves on Sym^(n+1)(C) due to
Kapranov-Schechtman. We show that any An-schober gives rise to a
categorical action of the Artin braid group Br_(n+1) and demonstrate how
this recovers familiar examples of such actions arising from Seidel-Thomas
An-configurations of spherical objects in categorical Picard-Lefschetz
theory and Rickard complexes in link homology theory. As a key example, we
use singular Soergel bimodules to construct a factorizing family of
An-schobers which we refer to as Soergel schobers. We expect such
families to give rise to a categorical analog of a graded bialgebra valued
in a suitably defined freely generated braided monoidal
(infinity,2)-category.
With Tobias Dyckerhoff.
28) Braiding on type A Soergel bimodules: semistrictness and naturality

We consider categories of Soergel bimodules for the symmetric groups S_n in their gl(n)-realizations for all n and assemble them into a locally linear monoidal bicategory. Chain complexes of Soergel bimodules likewise form a locally dg-monoidal bicategory which can be equipped with the structure of a braiding, whose data includes the Rouquier complexes of shuffle braids. The braiding, together with a uniqueness result, was established in an infinity-categorical setting in recent work with Yu Leon Liu, Aaron Mazel-Gee and David Reutter.
In the present article, we construct this braiding explicitly and describe its requisite coherent naturality structure in a concrete dg-model for the morphism categories. To this end, we first assemble the Elias-Khovanov-Williamson diagrammatic Hecke categories as well as categories of chain complexes thereover into locally linear semistrict monoidal 2-categories. Along the way, we prove strictness results for certain standard categorical constructions, which may be of independent interest. In a second step, we provide explicit (higher) homotopies for the naturality of the braiding with respect to generating morphisms of the Elias-Khovanov-Williamson diagrammatic calculus. Rather surprisingly, we observe hereby that higher homotopies appear already for height move relations of generating morphisms. Finally, we extend the homotopy-coherent naturality data for the braiding to all chain complexes using cohomology-vanishing arguments.
With Catharina Stroppel.
27) Bordered invariants from Khovanov homology
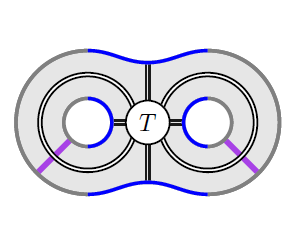
To every compact oriented surface that is
composed entirely out of 2-dimensional 0-
and 1-handles, we construct a dg category
using structures arising in Khovanov
homology. These dg categories form part of
the 2-dimensional layer (a.k.a. modular
functor) of a categorified version of the
sl(2) Turaev-Viro topological field theory.
As a byproduct, we obtain a unified
perspective on several hitherto disparate
constructions in categorified quantum
topology, including the Rozansky-Willis
invariants, Asaeda-Przytycki--Sikora
homologies for links in thickened surfaces,
categorified Jones-Wenzl projectors and
associated spin networks, and dg horizontal
traces.
With Matthew Hogancamp and David Rose.
26) Invariants of surfaces in smooth 4-manifolds from link homology
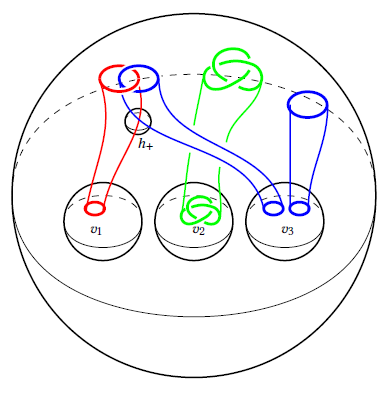
We construct analogs of Khovanov-Jacobsson classes and the Rasmussen invariant for links in the boundary of any smooth oriented 4-manifold. The main tools are skein lasagna modules based on equivariant and deformed versions of gl(N) link homology, for which we prove non-vanishing and decomposition results.
With Scott Morrison and Kevin Walker.
25) A braided (infinity,2)-category of Soergel bimodules
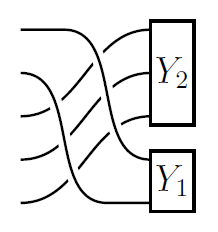
The Hecke algebras for all symmetric groups taken together form a braided monoidal category that controls all quantum link invariants of type A and, by extension, the standard canon of topological quantum field theories in dimension 3 and 4. Here we provide the first categorification of this Hecke braided monoidal category, which takes the form of an E2-monoidal (infinity,2)-category whose hom-(infinity,1)-categories are k-linear, stable, idempotent-complete, and equipped with Z-actions. This categorification is designed to control homotopy-coherent link homology theories and to-be-constructed topological quantum field theories in dimension 4 and 5. Our construction is based on chain complexes of Soergel bimodules, with monoidal structure given by parabolic induction and braiding implemented by Rouquier complexes, all modelled homotopy-coherently. This is part of a framework which allows to transfer the toolkit of the categorification literature into the realm of infinity-categories and higher algebra. Along the way, we develop families of factorization systems for (infinity,n)-categories, enriched infinity-categories, and infinity-operads, which may be of independent interest. As a service aimed at readers less familiar with homotopy-coherent mathematics, we include a brief introduction to the necessary infinity-categorical technology in the form of an appendix.
With Yu Leon Liu, Aaron Mazel-Gee, David Reutter, and Catharina Stroppel.
arXiv 2024
24) A Kirby color for Khovanov homology
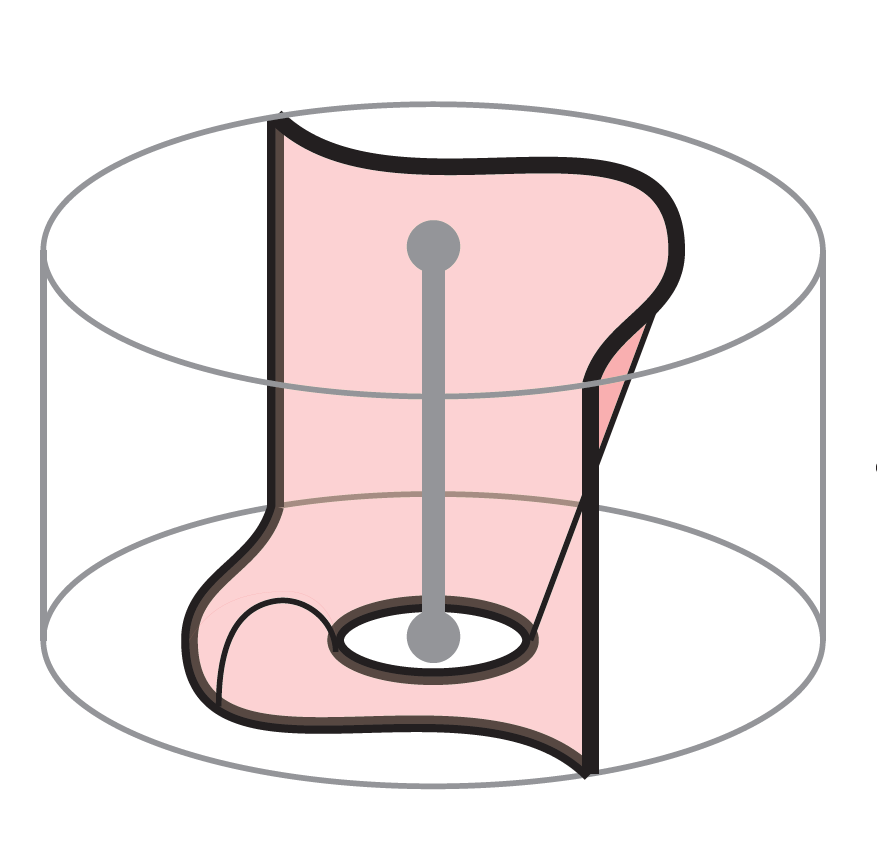
We construct a Kirby color in the setting of
Khovanov homology: an ind-object of the
annular Bar-Natan category that is equipped
with a natural handle slide isomorphism.
Using functoriality and cabling properties
of Khovanov homology, we define a
Kirby-colored Khovanov homology that is
invariant under the handle slide Kirby move,
up to isomorphism. Via the
Manolescu--Neithalath 2-handle formula,
Kirby-colored Khovanov homology agrees with
the gl(2) skein lasagna module, hence is an
invariant of 4-dimensional 2-handlebodies.
With Matthew Hogancamp and David Rose.
Journal of the European Mathematical Society (accepted, 2023)
23) Skein lasagna modules and handle decompositions
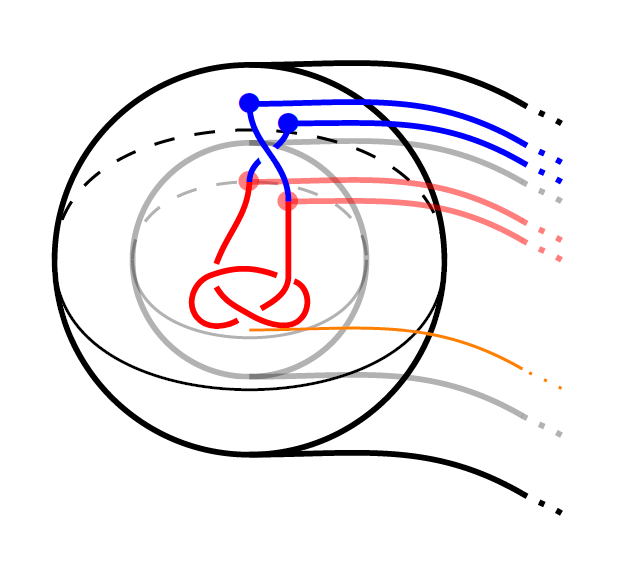
The skein lasagna module is an extension of
Khovanov-Rozansky homology to the setting
of a four-manifold and a link in its
boundary. This invariant plays the role of
the Hilbert space of an associated fully
extended (4+epsilon)-dimensional TQFT. We
give a general procedure for expressing the
skein lasagna module in terms of a handle
decomposition for the four-manifold. We use
this to calculate a few examples, and show
that the skein lasagna module can sometimes
be locally infinite dimensional.
With Ciprian Manolescu and Kevin Walker.
Advances in Mathematics 425 (2023) Paper No. 109071
22) Link splitting deformation of colored Khovanov-Rozansky homology
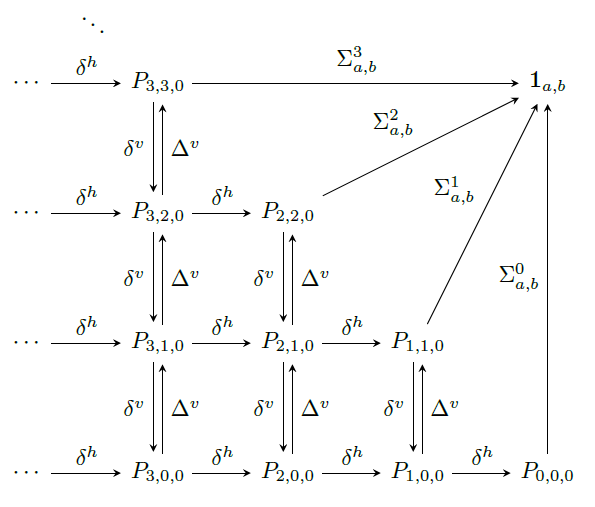
We introduce a multi-parameter deformation
of the triply-graded Khovanov-Rozansky
homology of links colored by one-column
Young diagrams, generalizing the "y-ified"
link homology of Gorsky-Hogancamp and work
of Cautis--Lauda--Sussan. For each link
component, the natural set of deformation
parameters corresponds to interpolation
coordinates on the Hilbert scheme of the
plane. We extend our deformed link homology
theory to braids by introducing a monoidal
dg 2-category of curved complexes of type A
singular Soergel bimodules. Using this
framework, we promote to the curved setting
the categorical colored skein relation from
arXiv:2107.08117
and also the notion of splitting map for the
colored full twists on two strands. As
applications, we compute the invariants of
colored Hopf links in terms of ideals
generated by Haiman determinants and use
these results to establish general link
splitting properties for our deformed,
colored, triply-graded link homology.
Informed by this, we formulate several
conjectures that have implications for the
relation between (colored)
Khovanov--Rozansky homology and Hilbert
schemes.
With Matthew Hogancamp and David Rose.
Proceedings of the London Mathematical Society (accepted, 2023)
21) A skein relation for singular Soergel bimodules
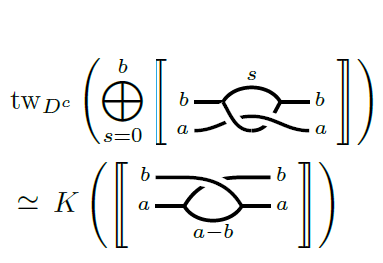
We study the skein relation that governs the
HOMFLYPT invariant of links colored by
one-column Young diagrams. Our main result
is a categorification of this colored skein
relation. This takes the form of a homotopy
equivalence between two one-sided twisted
complexes constructed from Rickard complexes
of singular Soergel bimodules associated to
braided webs. Along the way, we prove a
conjecture of Beliakova-Habiro relating the
colored 2-strand full twist complex with the
categorical ribbon element for quantum
sl(2).
With Matthew Hogancamp and David Rose.
20) SL2 tilting modules in the mixed case
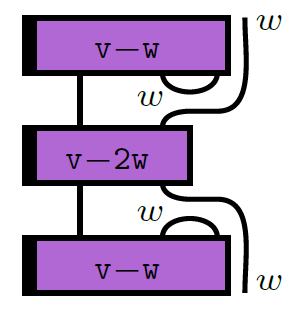
Using the non-semisimple Temperley-Lieb
calculus, we study the additive and monoidal
structure of the category of tilting modules
for SL2 in the mixed case. This
simultaneously generalizes the semisimple
situation, the case of the complex quantum
group at a root of unity, and the algebraic
group case in positive characteristic. We
describe character formulas and give a
presentation of the category of tilting
modules as an additive category via a quiver
with relations. Turning to the monoidal
structure, we describe fusion rules and
obtain an explicit recursive description of
the appropriate analog of Jones-Wenzl
projectors. We also discuss certain theta
values, the tensor ideals, mixed Verlinde
quotients and the non-degeneracy of the
braiding.
With Louise Sutton, Daniel Tubbenhauer, and Jieru Zhu.
Selecta Mathematica 29-3 (2023) Paper No. 39.
19) gl(2) foams and the Khovanov homotopy type
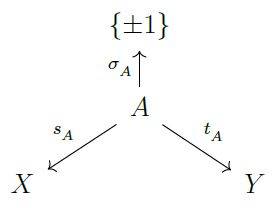
The Blanchet link homology theory is an
oriented model of Khovanov homology,
functorial over the integers with respect to
link cobordisms. We formulate a stable
homotopy refinement of the Blanchet theory,
based on a comparison of the Blanchet and
Khovanov chain complexes associated to link
diagrams. The construction of the stable
homotopy type relies on the signed Burnside
category approach of
Sarkar-Scaduto-Stoffregen.
With Vyacheslav Krushkal.
Indiana University Mathematics Journal 72-3 (2023) 731--755.
18) Tangle addition and the knots-quivers correspondence
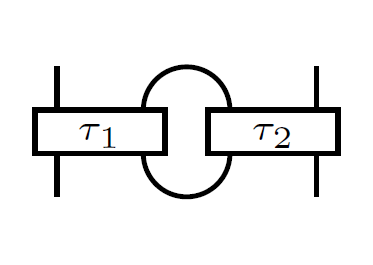
We prove that the generating functions for
the one row/column colored HOMFLY-PT
invariants of arborescent links are
specializations of the generating functions
of the motivic Donaldson-Thomas invariants
of appropriate quivers that we naturally
associate with these links. Our approach
extends the previously established
tangles-quivers correspondence for rational
tangles to algebraic tangles by developing
gluing formulas for HOMFLY-PT skein
generating functions under Conway's tangle
addition. As a consequence, we prove the
conjectural links-quivers correspondence of
Kucharski–Reineke–Stošić–Sułkowski
for all
arborescent links.
With Marko Stošić.
Journal of the London Mathematical Society 104-1 (2021) 341-361
17) The center of SL(2) tilting modules
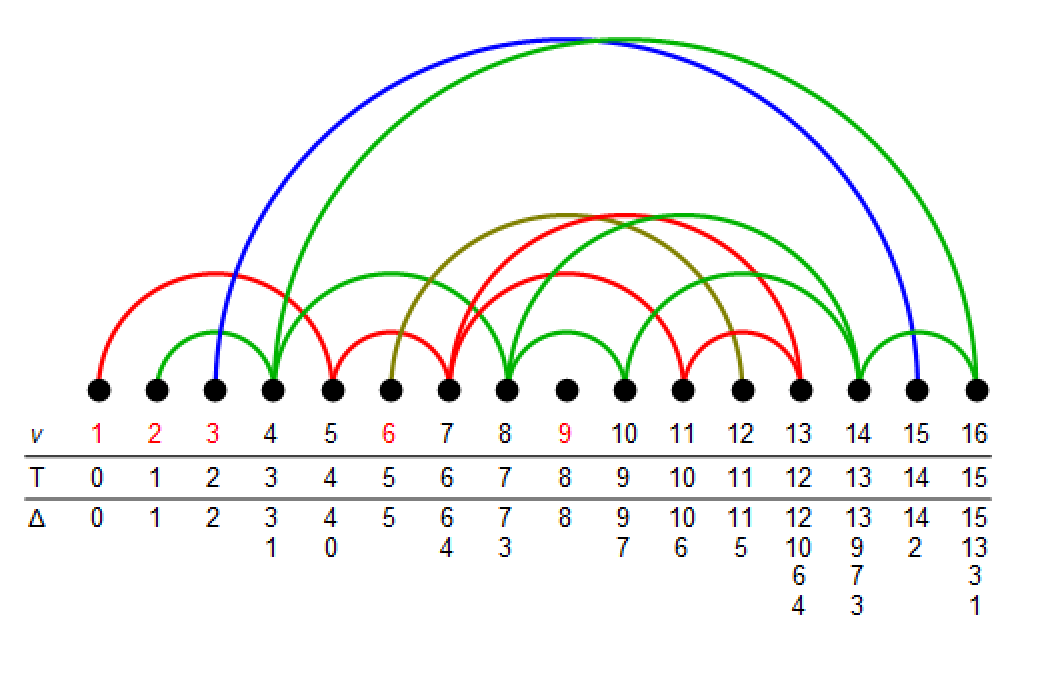
In this note we compute the centers of the
categories of tilting modules for
G=SL(2) in prime characteristic, of
tilting modules for the corresponding quantum
group at a complex root of unity, and of
projective G_gT-modules when g=1,2.
With Daniel Tubbenhauer.
Glasgow Mathematical Journal 64 (2022) 165-184
16) A coupled Temperley-Lieb algebra for the superintegrable chiral Potts chain

The hamiltonian of the N-state
superintegrable chiral Potts (SICP) model is
written in terms of a coupled algebra
defined by N-1 types of Temperley-Lieb
generators. This generalises a previous
result for N=3 obtained by J. F. Fjelstad
and T. Månsson [J. Phys. A 45
(2012) 155208]. A pictorial representation
of a related coupled algebra is given for the
N=3 case which involves a generalisation
of the pictorial representation of the
Temperley-Lieb algebra to include a pole
around which loops can become entangled.
(shortened)
With Remy Adderton and Murray T. Batchelor.
Journal of Physics A: Mathematical and Theoretical 53-36 (2020)
15) Derived traces of Soergel categories
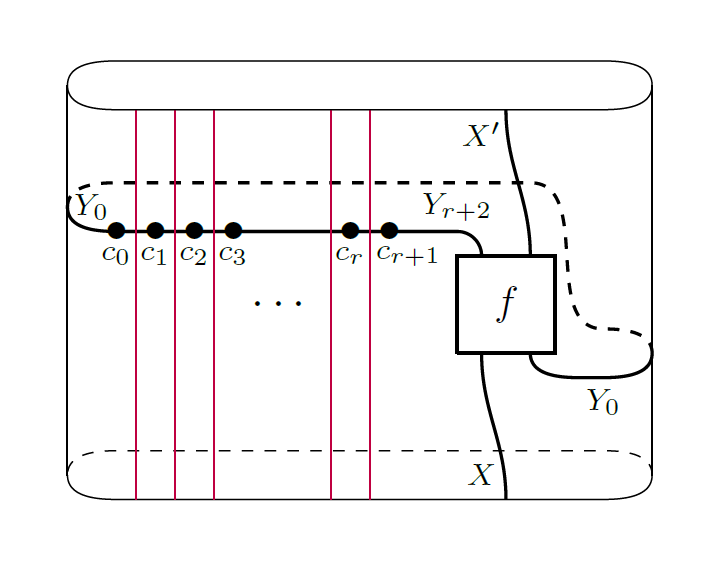
We study two kinds of categorical traces of (monoidal)
dg categories, with particular interest in categories of
Soergel bimodules. First, we explicitly compute the
usual Hochschild homology, or derived vertical trace, of
the category of Soergel bimodules in arbitrary types.
Secondly, we introduce the notion of derived horizontal
trace of a monoidal dg category and compute the derived
horizontal trace of Soergel bimodules in type $A$. As
an application we obtain a derived annular
Khovanov--Rozansky link invariant with an action of full
twist insertion, and thus a categorification of the
HOMFLY-PT skein module of the solid torus.
With Eugene Gorsky and Matthew Hogancamp.
International Mathematics Research Notices
published online
14) Invariants of 4-manifolds from Khovanov-Rozansky link homology
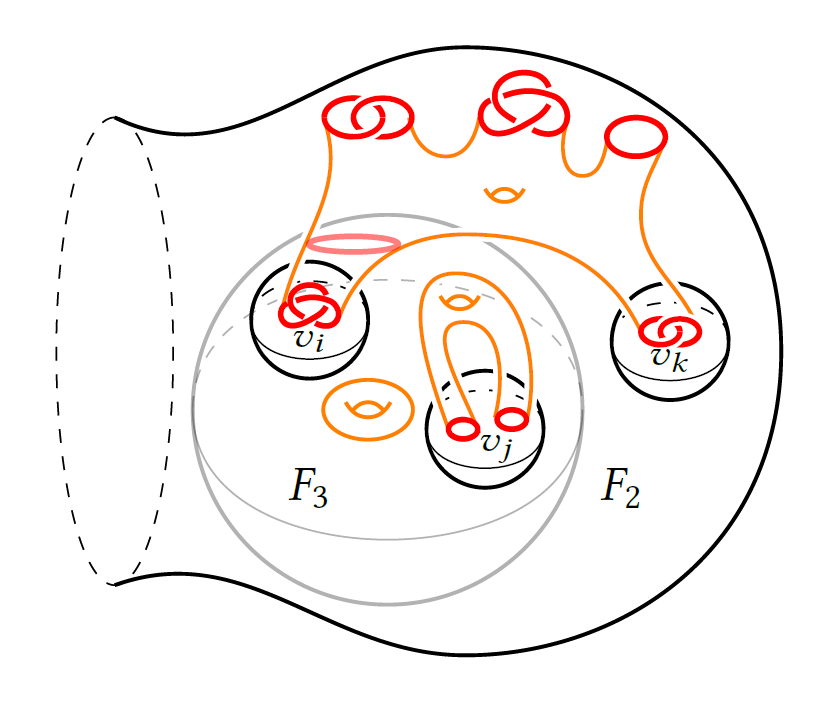
We use Khovanov-Rozansky gl(N) link homology to define invariants of oriented smooth 4-manifolds, as skein modules constructed from certain 4-categories with well-behaved duals. The technical heart of this construction is a proof of the sweep-around property, which makes these link homologies well defined in the 3-sphere.
With Scott Morrison and Kevin Walker.
Accepted for publication in Geometry & Topology 26-8 (2022) 3367--3420.
13) Quivers for SL(2) tilting modules

Using diagrammatic methods, we define a quiver algebra depending on a prime p and show
that it is the algebra underlying the category of tilting modules for SL(2) in
characteristic p. Along the way we obtain a presentation for morphisms between
p-Jones-Wenzl projectors.
With Daniel Tubbenhauer.
Representation Theory 25 (2021) 440-480
12) Evaluations of annular Khovanov-Rozansky homology
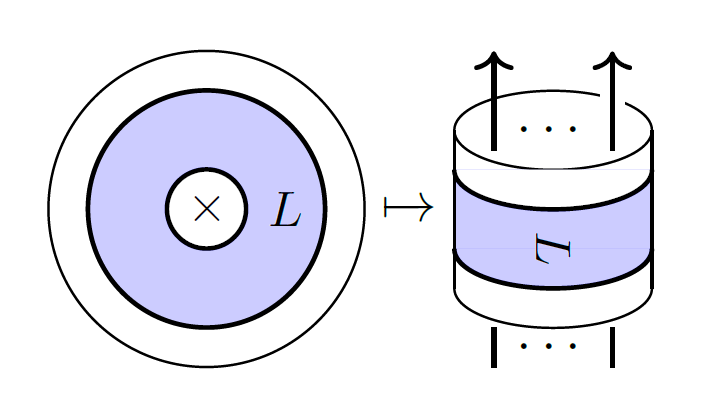
We describe the universal target of annular Khovanov-Rozansky link homology functors as
the homotopy category of a free symmetric monoidal category generated by one object and
one endomorphism. This categorifies the ring of symmetric functions and admits
categorical analogues of plethystic transformations, which we use to characterize the
annular invariants of Coxeter braids. Further, we prove the existence of symmetric group
actions on the Khovanov-Rozansky invariants of cabled tangles and we introduce spectral
sequences that aid in computing the homologies of generalized Hopf links. Finally, we
conjecture a characterization of the horizontal traces of Rouquier complexes of Coxeter
braids in other types.
With Eugene Gorsky.
Math Z. 303-25 (2023)
11) Algèbre diagrammatique et catégorification
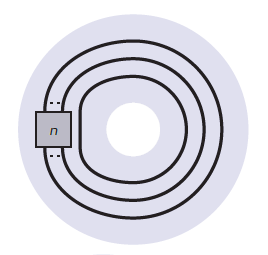
Nous proposons une illustration diagrammatique
abordable du concept de catégorification qui s’est
développé au cours des vingt dernières années.
A friendly outreach article in French, written mostly by Hoel
Queffelec, inspired by our joint work.
La Gazette des mathématiciens 163 (janvier 2020)
10) Khovanov homology and categorification of skein modules
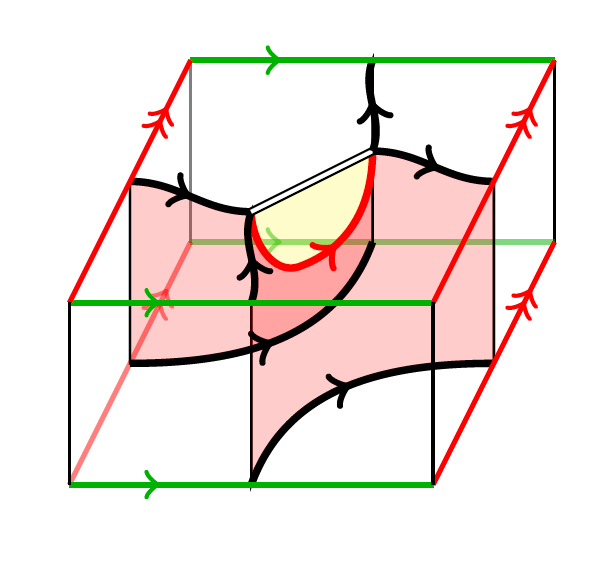
For every oriented surface of finite type, we construct a functorial Khovanov homology
for links in a thickening of the surface, which takes values in a categorification of
the corresponding gl(2) skein module. The latter is a mild refinement of the Kauffman
bracket skein algebra, and its categorification is constructed using a category of gl(2)
foams that admits an interesting non-negative grading. We expect that the natural
algebra structure on the gl(2) skein module can be categorified by a tensor product that
makes the surface link homology functor monoidal. We construct a candidate bifunctor on
the target category and conjecture that it extends to a monoidal structure. This would
give rise to a canonical basis of the associated gl(2) skein algebra and verify an
analogue of a positivity conjecture of Fock–Goncharov and Turston. We provide evidence
towards the monoidality conjecture by checking several instances of a categorified
Frohman-Gelca formula for the skein algebra of the torus. Finally, we recover a variant
of the Asaeda–Przytycki–Sikora surface link homologies and prove that surface embeddings
give rise to spectral sequences between them.
With Hoel
Queffelec
Quantum Topology 21-1 (2021) 129-209.
9) Extremal weight projectors II
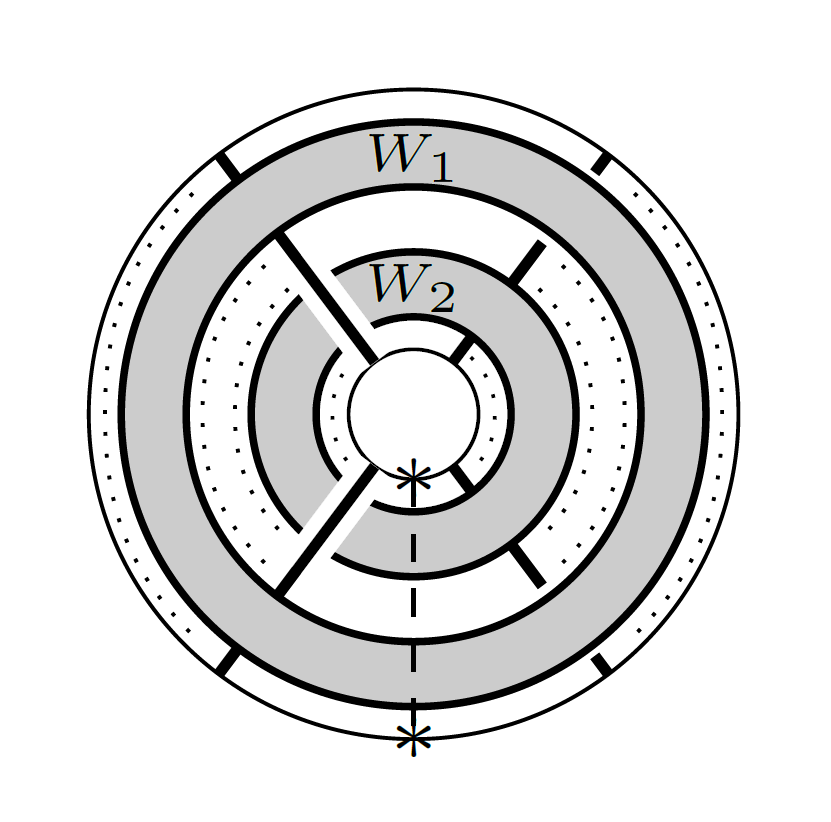
In previous work, we have constructed diagrammatic idempotents in an affine extension of
the Temperley–Lieb category, which describe extremal weight projectors for sl(2), and
which categorify Chebyshev polynomials of the first kind. In this paper, we generalize
the construction of extremal weight projectors to the case of gl(N) for N > 1, with a
view towards categorifying the corresponding torus skein algebras via Khovanov–Rozansky
link homology. As by-products, we obtain compatible diagrammatic presentations of the
representation categories of gl(N) and its Cartan subalgebra, and a categorification of
power-sum symmetric polynomials.
With Hoel
Queffelec.
Algebraic Combinatorics (accepted, 2023)
8) Rational links and DT invariants of quivers
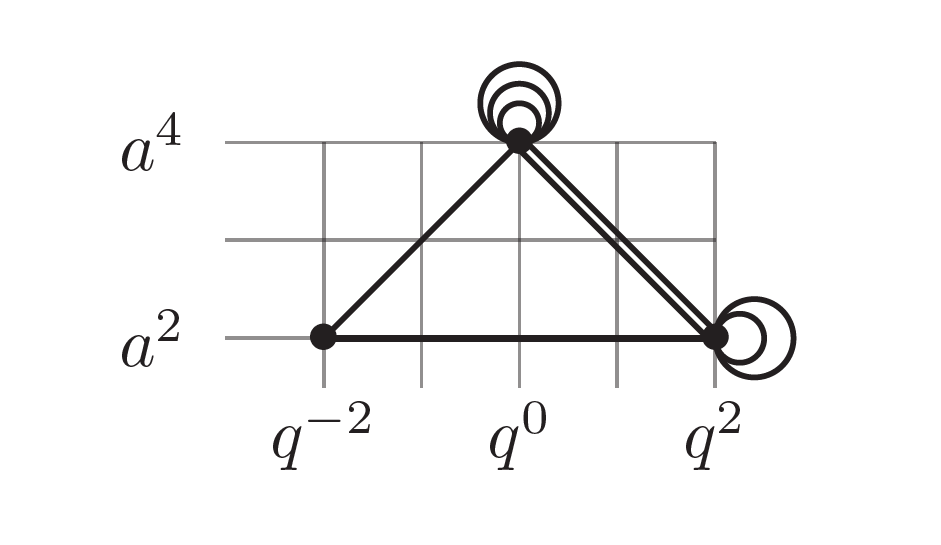
We prove that the generating functions for the colored HOMFLY-PT polynomials of rational
links are specializations of the generating functions of the motivic Donaldson-Thomas
invariants of appropriate quivers that we naturally associate with these links. This
shows that the conjectural links-quivers correspondence of
Kucharski–Reineke–Stošić–Sułkowski as well as the LMOV conjecture hold
for rational links. Along the way, we extend the links-quivers correspondence to tangles
and, thus, explore elements of a skein theory for motivic Donaldson-Thomas invariants.
With Marko Stošić.
International Mathematical Research Notices 6 (2021) 4169-4210.
7) Functoriality of colored link homologies
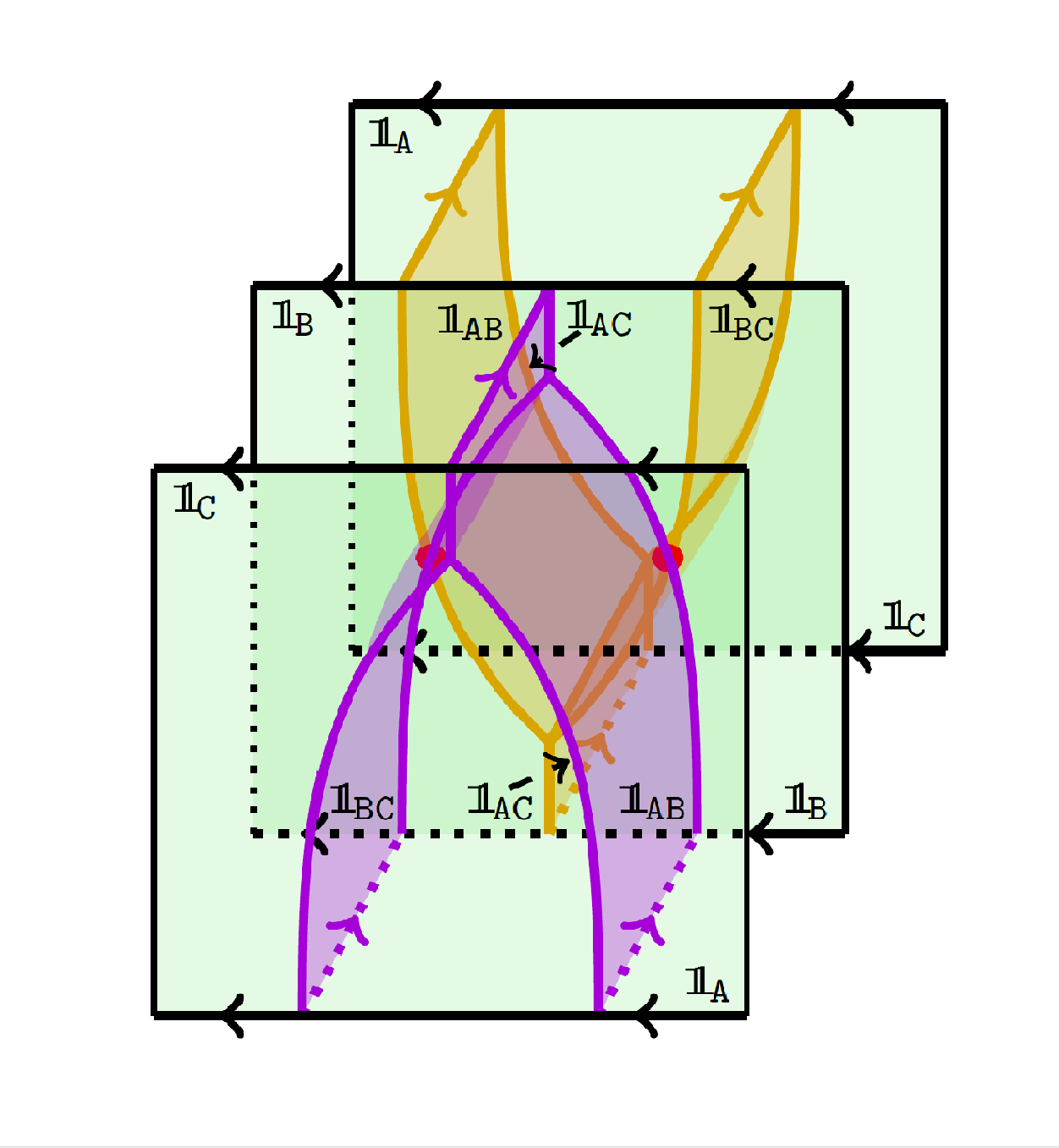
We prove that the bigraded, colored Khovanov–Rozansky type A link and tangle invariants
are functorial with respect to link and tangle cobordisms.
With Michael Ehrig
and Daniel Tubbenhauer.
Proceedings of the London Mathematical Society 117-5 (2018), 996-1040
6) Extremal weight projectors
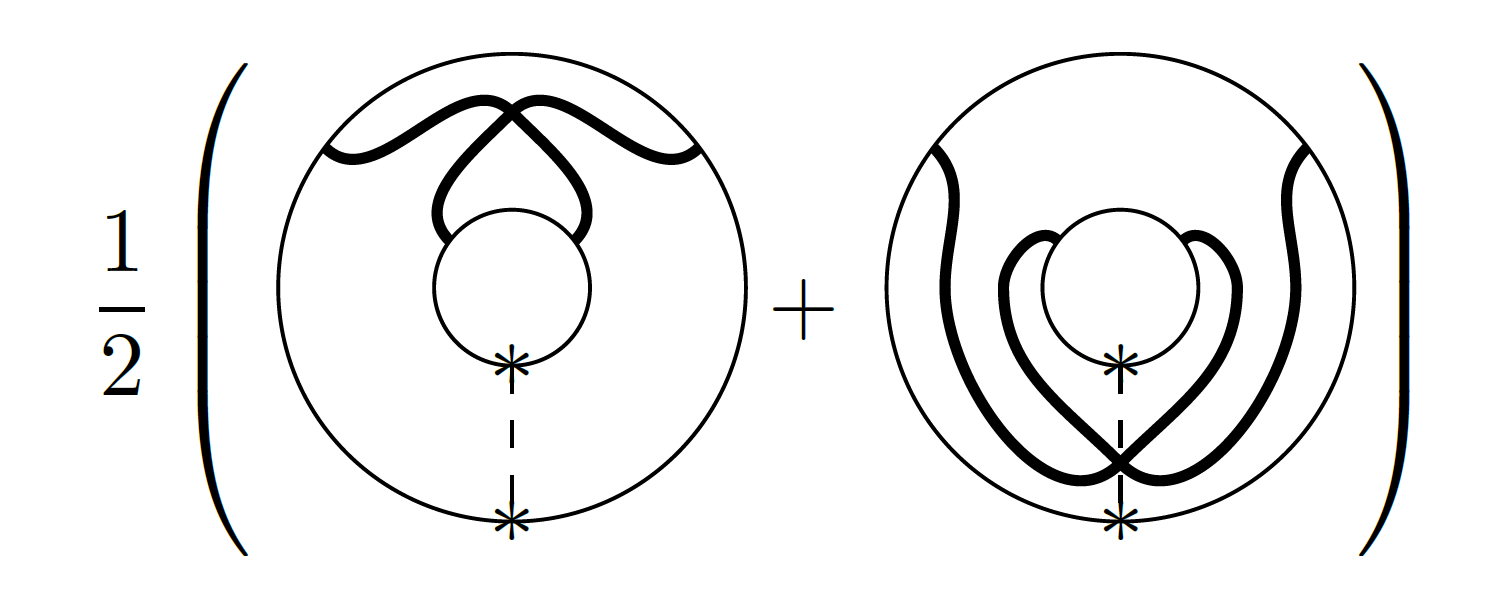
We introduce a quotient of the affine Temperley-Lieb category that encodes all weight
preserving linear maps between finite-dimensional sl(2)-representations. We study the
diagrammatic idempotents that correspond to projections onto extremal weight spaces and
find that they satisfy similar properties as Jones-Wenzl projectors, and that they
categorify the Chebyshev polynomials of the first kind. This gives a categorification of
the Kauffman bracket skein algebra of the annulus, which is well adapted to the task of
categorifying the multiplication on the Kauffman bracket skein module of the torus.
With Hoel
Queffelec.
Mathematical Research Letters 25-6 (2018), 1911-1936
5) Exponential growth of colored HOMFLY-PT homology
We define reduced colored sl(N) link homologies and use deformation spectral sequences to
characterize their dependence on color and rank. We then define reduced colored
HOMFLY-PT homologies and prove that they arise as large N limits of sl(N) homologies.
Together, these results allow proofs of many aspects of the physically conjectured
structure of the family of type A link homologies. In particular, we verify a conjecture
of Gorsky, Gukov and Stošić about the growth of colored HOMFLY-PT
homologies.
Advances in Mathematics 353 (2019), 471-525
4) Super q-Howe duality and web categories
We use super q–Howe duality to provide diagrammatic presentations of an idempotented form
of the Hecke algebra and of categories of gl(N)–modules (and, more generally,
gl(N|M)–modules) whose objects are tensor generated by exterior and symmetric powers of
the vector representations. As an application, we give a representation-theoretic
explanation and a diagrammatic version of a known symmetry of colored HOMFLY–PT
polynomials.
With Daniel Tubbenhauer and Pedro Vaz.
Algebraic & Geometric Topology 17-6 (2017), 3703-3749
3) Deformations of colored sl(N) link homologies via foams
We prove a conjectured decomposition of deformed sl(N) link homology, as well as an
extension to the case of colored links, generalizing results of Lee, Gornik, and Wu. To
this end, we use foam technology to give a completely combinatorial construction of Wu’s
deformed colored sl(N) link homologies. By studying the underlying deformed higher
representation-theoretic structures and generalizing the Karoubi envelope approach of
Bar-Natan and Morrison, we explicitly compute the deformed invariants in terms of
undeformed type A link homologies of lower rank and color.
With David Rose.
Geometry & Topology 20-6 (2016), 3431-3517
2) q-holonomic formulas for colored HOMFLY polynomials of 2-bridge links
We compute q-holonomic formulas for the HOMFLY polynomials of 2-bridge links colored with
one-column (or one-row) Young diagrams.
Journal of Pure and Applied Algebra 223-4 (2019), 1434-1439
1) Categorified sl(N) invariants of colored rational tangles
We use categorical skew Howe duality to find recursion rules that compute categorified
sl(N) invariants of rational tangles colored by exterior powers of the standard
representation. Further, we offer a geometric interpretation of these rules which
suggests a connection to Floer theory. Along the way we make progress towards two
conjectures about the colored HOMFLY homology of rational links and discuss consequences
for the corresponding decategorified invariants.
Algebraic & Geometric Topology 16-1 (2016), 427-482

 © UHH, RRZ/MCC, Mentz
© UHH, RRZ/MCC, Mentz














